단단한 강화 학습 2장 다중 선택 2.6 ~ 정리
단단한 강화 학습 2장 다중 선택 2.6 ~ 정리
2.6 Optimal Initial Value
Exploration을 촉진하는 기법을 긍정적 초깃값(Optimal initial value)라고 부른다.
이전에 언급된 방법들은 행동 가치의 초기 추정값 $Q_1(a)$의 영향을 받았다. 초깃값에 편중 되어(Biased) 있었다. 편향 되었다는게 나쁜 것만은 아니다. 편향된 정보를 사전 지식으로 초기 추정값을 정할 수 있는 장점이 있다.
액션 들의 가치에 대한 초기 추정값이 긍정적이면, 학습자는 액션에 대한 보상값에 실망해서 다른 행동을 선택하게 된다. 결과적으로 가치 추정값이 수렴하기 전까지 Exploration이 된다.
아래의 그림은 이전의 10-Armed Bandits에서 모든 행동 a에 대해
- $Q_1(a) = 5$를 사용한 그리디 메소드
- $Q_1(a) = 0$을 사용한 입실론 그리디 메소드
를 적용 했을 때 결과를 함께 보여준다. 실험 초기에는 탐험이 많은 그리디 방법이 안좋은 결과를 보이지만, 시간이 지남에 따라 Exploration이 줄어들기 때문에 궁극적으로는 더 좋은 성능을 보여준다.
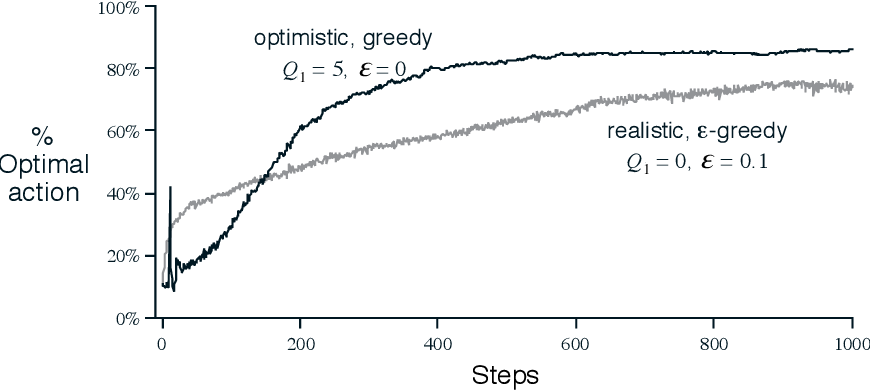
Figure 1
하지만 초기 조건에 맞춘다면 비정상적(non-stationary)문제에는 도움이 되지 않는다. 초깃값에 의존하는 것은 아래와 같은 문제가 있다.
- Exploration에 대한 원동력이 본질적으로 일시적이다.
- 새로운 Action에 대해서도 Exploration이 필요하다.
그렇기 때문에 초기 조건에 너무 많이 초점을 맞추는 것은 좋지 않다는 결론을 얻을 수 있다.
2.7 Upper Confidence Bound Action Selection
입실론 그리디 방법은 비 탐욕적 행동을 선택하는 것을 강제하지만, 행동을 선택할 때 탐욕적 행동과 아닌 것 중 어느 쪽도 선호하지 않고 선택한다.
- 행동 가치의 추정값이 최대치에 얼마나 가까운지?
- 추정의 불확실성이 얼마인지?
를 고려하는 것이 중요하다. 아래의 식은 효과적인 행동 선택 방법 한가지를 제안한다.
$A_t \doteq \underset{a}{arg \ max} \ [ Q_t(a) + c \sqrt{\frac{ln \ t}{N_t(a)}}]$
- $ln \ t$ : 시각 t 에 대한 자연 로그
- $N_t(a)$ : 시각 t 이전의 행동 a를 선택한 횟수
- $c > 0$ : 불확실성의 정도 ( Exploration의 정도 )
행동 a의 가치에 대한 추정값의 불확실성 또는 편차를 함께 고려한다. 위 식의 최댓값은 행동 a의 가치로 사용가능한 값들의 상한값(Maximum Bound)이 되며, 파라미터 c를 사용해서 상한의 신뢰 수준을 결정한다. 특정 액션 a가 선택될 때마다 불확실성은 다음과 같이 변화한다.
- a 가 선택 될 때, 분모의 $N_t(a)$가 증가하면서 불확실성이 감소한다.
- a 가 선택 되지 않을 때, $ln \ t$ 만 증가하면서 불확실성이 증가한다.
모든 행동이 선택 되지만 더 작은 가치 추정값을 갖는 행동이나 이미 자주 선택된 행동은 시간이 지남에 따라 선택되는 빈도수가 작아진다.
아래의 그림은 마찬가지로 10-Armed Bandit에서 UCB를 적용한 결과이다. 처음을 제외하면 일반적으로 UCB가 성능이 더 좋다.
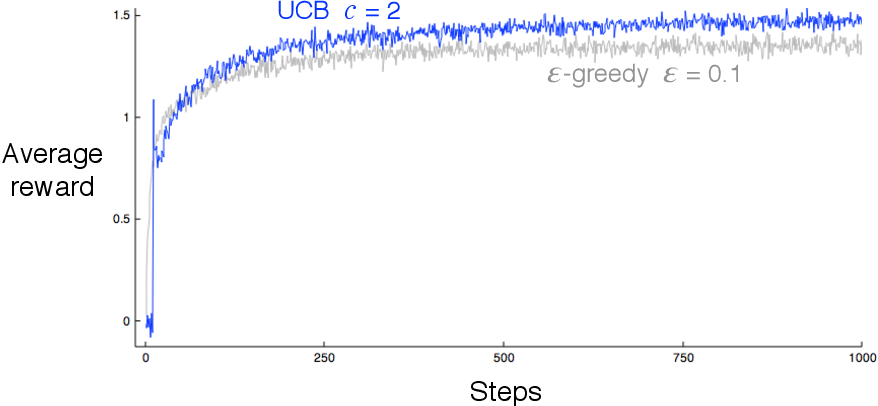
Figure 2
책의 뒷 부분에서 다루는 UCB를 더 일반적인 강화학습 문제로 확장하는 방법은 입실론 그리디 방법보다 어렵다. nonstationary 문제를 다루고 더 큰 상태 공간을 다루기 때문이다.
2.8 Gradient Bandit Algorithm
각 행동 a에 대한 수치적 선호도(preference)를 학습하는 방법이다. 행동의 가치를 추정하는 방법이 아니라 선호도를 기반으로 행동을 선택하는 방법이다. 선호도($H_t(a)$)가 큰 행동이 더 자주 선택된다. 선호도는 보상과는 다른 개념이다.
각 행동을 선택할 확률은 $소프트 \ 맥스 \ 분포_{soft-max \ distribution(Gibbs \ 또는 \ Boltzman \ 분포)}$에 따라 다음과 같이 결정된다.
$Pr {\{ A_t = a}\} \doteq \frac{e^{H_t(a)}}{\sum_{b=1}^k e^{H_t(b)}} \doteq \pi_t(a)$
- $\pi_t(a)$ : 시각 t에 행동 a를 선택할 확률
- $H_1(a) = 0$ : 처음의 모든 행동 선호도는 같다.
확률론적 경사도 증가(stochastic gradient ascent)방법을 활용하는 학습 알고리즘으로 행동 $A_t$를 선택한 후에 보상 $R_i$를 받는 모든 단계에 대한 선호도를 아래와 같이 갱신한다.
$H_{t+1}(A_t) \doteq H_t(A_t) + \alpha(R_t - \bar{R_t})(1-\pi_t(A_t))$ 그리고
$H_{t+1}(a) \doteq H_t(a) - \alpha(R_t - \bar{R_t})\pi_t(a)$ 모든 $a \neq A_t$에 대해
- $\alpha > 0$ : 시간 간격의 크기
- $\bar{R_t} \in R$ : 시간 t 까지의 모든 보상에 대한 평균
현재의 보상과 비교하는 대상으로 $\bar{R_t}$를 사용한다.
- $R_t > \bar{R_t}$ 인 경우, 미래에 $A_t$를 선택할 확률 $\pi_{t+1}(a)$이 증가한다.
- $R_t < \bar{R_t}$ 인 경우, 미래에 $A_t$를 선택할 확률 $\pi_{t+1}(a)$이 감소한다.
선택된 행동에 대한 확률은 증가하고, 선택 되지 않는 행동에 대한 확률은 반대로 변화한다.
아래의 그림은 마찬가지로 10-Armed Bandit에서 Gradient Bandit 알고리즘을 적용한 결과이다. 평균 4, 분산 1인 정규분포로 보상의 참값이 선택된다.
- 비교 대상이 있는 경우 ( with baseline )
- 비교 대상이 없는 경우 ( without baseline )
에 대해서 결과를 보이는데 비교 대상이 없는 경우에는 성능이 상당히 저하된다.
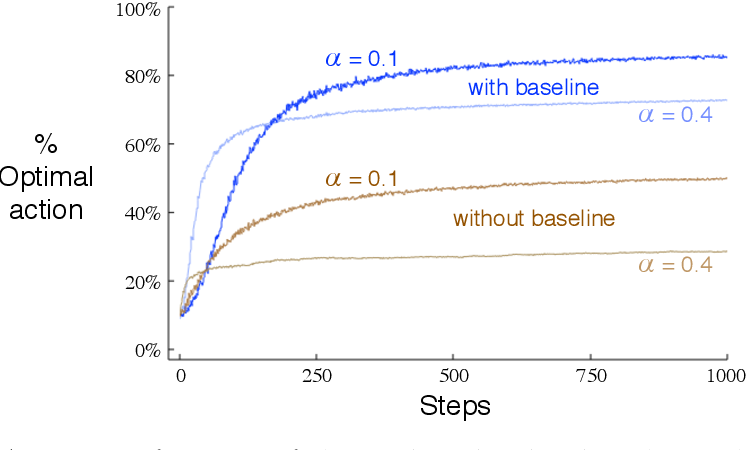
Figure 3
경사도 증가(gradient ascent) 규칙을 따르면, 행동의 선호도 $H_t(a)$의 증가량은 선호도 증가가 성능에 미치는 효과와 비례한다.
$H_{t+1}(a) \doteq H_t(a) + \alpha\frac{\partial E[R_t]}{\partial H_t(a)}$
여기서 $E[R_t]$인 성능 측정 값은 보상의 기댓값이 된다.
$E[R_t] = \underset{x}\sum\pi_t(x)q_*(x)$
선호도 증가가 성능에 미치는 효과의 측정은 이 성능 지표를 행동의 선호도를 $편미분_{partial \ derivative}$한 것을 통해 이루어진다. 성능의 경사돗값(gradient)에 대해 살펴보면
$\frac{\partial E[R_t]}{\partial H_t(a)} = \frac{\partial}{\partial H_t(a)}[\underset{x}\sum\pi_t(x)q_*(x)] = \underset{x}\sum{q_*(x)\frac{\partial \pi_t(x)}{\partial H_t(a)}} = \underset{x}\sum{(q_*(x) - B_t)\frac{\partial\pi_t(x)}{\partial H_t(a)}}$
- $B_t$ : 비교 대상 ( Baseline )
비교 대상을 포함해도 등식에 변화가 없는게, 모든 행동에 대한 경사돗값의 총합이 0이다.
$\sum_x \frac{\partial \pi_t(x)}{\partial H_t(a)} = 0$
$H_t(a)$가 변함에 따라 어떤 행동을 선택할 확률은 증가하고 다른 행동을 선택할 확률은 감소하겠지만, 확률의 합은 1이기 때문에 행동을 선택할 확률의 증가와 감소의 총합은 항상 0이 된다. 따라서
$= E [(q_*(A_t) - B_t)\frac{\partial \pi_t(A_t)}{\partial H_t(a)} /\pi_t(A_t)]$
$= E [(R_t - \bar{R_t})\frac{\partial \pi_t(A_t)}{\partial H_t(a)} /\pi_t(A_t)]$
바로 $\frac{\partial \pi_t(A_t)}{\partial H_t(a)} = \pi_t(x)(1_{a=x} - \pi_t(a))$을 얻을 수 있다.
-
$a = x$ 일 경우, $1_{a=x} = 1$ 이 된다.
-
$a \neq x$ 일 경우, $1_{a=x} = 0$ 이 된다.
$= E [(R_t - \bar{R_t})\pi_t(A_t)(1_{a=A_t} - \pi_t(a))/\pi_t(A_t)]$ $= E [(R_t - \bar{R_t})(1_{a=A_t} - \pi_t(a))]$
계획 : 경사돗값을 각 단계에서 추출한 어떤 표본의 기댓값(표본평균)으로 표현하는 것
성능의 경사돗값을 위의 표본평균으로 대체하면 다음과 같은 수식이 된다.
모든 a에 대해 $H_{t+1}(a) = \alpha(R_t - \bar{R_t})(1_{a=A_t} - \pi_t(a))$
$\frac{\partial \pi_t(A_t)}{\partial H_t(a)} = \pi_t(x)(1_{a=x} - \pi_t(a))$의 성립함을 보여야 한다.
몫의 미분 법 $\frac{\partial}{\partial x}[\frac{f(x)}{g(x)}] = \frac{\frac{\partial f(x)}{\partial x}g(x)-f(x) \frac{\partial g(x)}{\partial x}}{g(x)^2}$을 그대로 적용하면
$\frac{\partial \pi_t(x)}{\partial H_t(a)} = \frac{\partial}{\partial H_t(a)}\pi_t(x)$
$= \frac{\partial}{\partial H_t(a)}[\frac{e^{H_t(x)}}{\sum^k_{y=1} e^{H_t(y)}}]$
$= \frac{\frac{\partial e^{H_t(x)}}{\partial H_t(a)}\sum^k_{y=1}e^{H_t(y)}-e^{H_t(x)}\frac{\partial \sum_{y=1}^k e^{H_t(y)}}{\partial H_t(a)}}{(\sum^k_{y=1} e^{H_t(y)})^2}$
$= \frac{1_{a=x}e^{H_t(x)}\sum_{y=1}^k e^{H_t(y)} - e^{H_t(x)}e^{H_t(a)}}{(\sum_{y=1}^k e^{H_t(y)})^2}$
$= \frac{1_{a=x}e^{H_t(x)}}{\sum_{y=1}^k e^{H_t(y)}} - \frac{e^{H_t(x)}e^{H_t(a)}}{(\sum_{y=1}^k e^{H_t(y)})^2}$
$= 1_{a=x}\pi_t(x) - \pi_t(x)\pi_t(a)$
$= \pi_t(x)(1_{a=x} - \pi_t(a))$
위 과정으로 두가지를 확인할 수 있다.
- 경사도 다중 선택 알고리즘의 갱신의 기댓값 = 보상의 기댓값에 대한 경사돗값
- 알고리즘이 확률론적 경사도 증가의 한 종류이다.
확률론적 경사도 증가의 한 종류라는 것은 강건한 수렴성을 갖는다는 것을 보장한다. 비교대상값의 특성에 대해서 어떠한 전제 조건도 없다. 그래도 이 알고리즘은 여전히 확률론적 경사도 증가의 한 종류가 된다.
추가로 비교대상값(Baseline)을 어떤 것을 선택하느냐는 갱신되는 값의 기댓값에 영향을 주지 않지만 갱신되는 값의 분산에는 영향을 주고 분산으로 인해 기댓값의 수렴 속도가 영향을 받는다.
2.9 Associative Search (Contextual Bandits)
일반적인 강화학습 문제에서는 고려해야할 여러 상황이 있고 강화학습의 목적은 정책을 학습하는 것이다.
정책 : 어떠한 상황으로부터 그 상황에 맞는 최고의 행동을 도출하는 대응 관계
연관 탐색 (associative search)
시행착오 학습으로 최고의 행동을 탐색하는 동시에 이 행동이 최고가 되는 상황을 이 행동과 연관시킨다. 이것을 맥락적 다중 선택(contextual bandits)이라고도 한다. Contextual Bandit은 완전한 강화 학습이라고도 할 수 없고 완전한 다중 선택 문제라고도 할 수 없지만 아래와 같은 유사성은 있다.
- 정책에 대한 학습을 포함한다. ( 강화 학습과 같음 )
- 행동이 그 순간의 보상에만 영향을 준다 ( 다중 선택 문제와 같음 )
2.10 요약
Exploration과 Exploitaion의 Trade-Off를 해결하기 위한 여러가지 간단한 방법을 제시했다.
- 입실론 그리디 : 좁은 시간 구역을 무작위로 선택
- UCB : 행동을 선택할 때 결정론적 방법을 취하지만, 각 단계에서 그때까지 얻은 표본의 수가 적은 행동을 미묘하게 선택한다.
- 경사도 다중 선택 : 행동의 선호도를 추정하고 소프트 맥스 분포를 활용해서 등급에 따른 확률적 방식으로 선호되는 행동을 선택한다.
- 초기 추정값 : 초깃값을 긍정적으로 설정하는 방법으로 그리디 한 방법에 Exploration을 추가한다.
위의 방법 중 가장 좋은 알고리즘을 선택하는 것은 문제가 있는데 모두 파라미터를 가지고 있다. 파라미터에 따라 성능이 달라지므로 각 시간 단계에 대한 평균값으로 완전한 학습 곡선(learning curve)를 그린다. U자를 뒤집어 놓은 모양으로 최적의 파라미터는 중간 정도에 위치한다는 것으로 판단할 수 있다. 물론 파라미터의 변화에 따라 얼마나 성능이 변화하는지도 평가해야한다. 다중 선택 문제에서는 전반적으로 UCB가 가장 좋은 성능을 보였다.
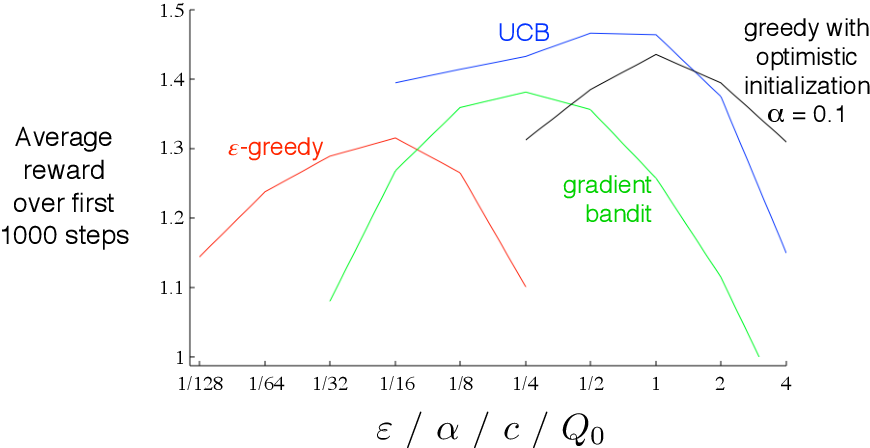
Figure 4
기틴스 인덱스 ( Gittins index )
다중 선택 문제에서 Exploration과 Exploitation 딜레마를 해결하는 방법은 특별한 행동 가치를 계산하는 것이다.
기틴스 인덱스는 행동 가치의 초기 분포에 대한 지식에 기반해서 각 단계 이후에 분포를 정확히 갱신하는 베이지안 방법의 일종인데 베이지안은 정보 업데이트를 위한 계산이 복잡할 수 있지만, 켤레 사전 분포(Conjugate Prior Distribution)라는 특별한 분포를 사용해서 쉽게 계산할 수 있다.
계산을 한 후, 각 단계에서 어떤 행동이 최선의 행동이 될 것인지에 대한 사후 확률(posterior probability)에 따라 행동을 선택한다. 사후 표본추출(posterior sampling)또는 톰슨 표본추출(Thompson sampling)이라고 불리는 이 방법은 분포와 관계없는(distribution-free) 방법이 보여주는 가장 좋은 성능과 대체로 유사한 성능을 보여준다.
베이지안 환경으로 Exploration과 Exploration 사이의 최적 균형을 계산하는 것도 가능하다. 모든 가능한 행동에 대해 즉각적으로 주어질 수 있는 보상의 확률과 그에 따른 행동 가치에 대한 사후 분포를 계산할 수 있다. 따라서 그 중 가장 좋은 것을 선택하기만 하면 된다. 하지만 두개의 행동과 두개의 보상이 있더라도 총 1000번의 타임 스탬프인 경우 계산량이 $2^{2000}$으로 실현 불가능한 양이다. 하지만 근삿값을 효율적으로 계산하는 것은 가능하다. 이러한 접근법으로 다중 선택 문제가 완전한 강화 학습의 한 종류가 되게끔 효과적으로 변화시킬 수 있다.